
Multiplication matrice-vecteur
Soit l'opération suivante à effectuer :
Un processeur incohérent entièrement parallèle de multiplication matrice-vecteur est illustré dans la figure II-21.
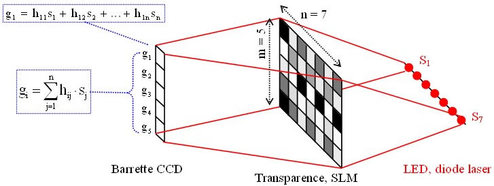
Dans cette figure on omet temporairement les détails des éléments optiques utilisés. L'intensité de la source Si est proportionnelle aux éléments des vecteurs si . Alors que la transmittance de la cellule hij dans le SLM est proportionnelle à l'élément hij de la matrice. Le ième élément de la barrette CCD en sortie reçoit une intensité lumineuse proportionnelle au signal :
Ce qui représente le résultat de la multiplication.
Pour que les faisceaux puissent se répandre verticalement et se focaliser horizontalement suivant des nappes on utilise une combinaison de lentilles sphériques et cylindriques accolées de même focales (voir figure II-22).
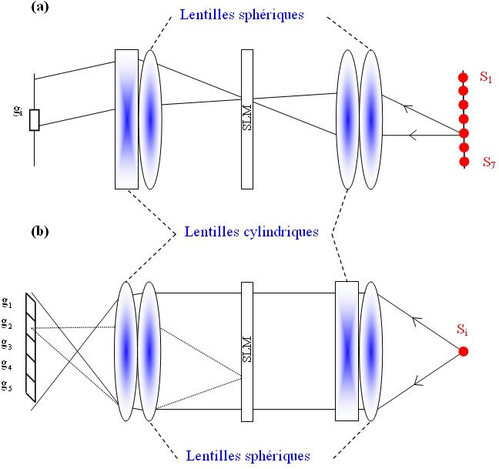
Cette combinaison possède une focale de f/2 dans la direction où la lentille cylindrique fait converger les rayons, et une focale de f dans la direction où la lentille cylindrique n'a aucune action. Ainsi on peut voir dans la figure II-22(a) que pour une nappe horizontale les sources sont imagées dans le plan contenant le SLM. Ensuite le faisceau est collimaté puisque la deuxième lentille cylindrique, tournée de 90° par rapport à la première, n'a aucune puissance convergente dans cette direction la focale équivalente de la deuxième paire de lentilles est de f). La vue de côté montrée dans la figure II-22(b) montre comment d'abord le faisceau est collimaté suivant une nappe verticale et ensuite à l'aide de la deuxième paire de lentilles on fait l'image de chaque colonne du SLM dans la barrette.
-
Ici le calcul se fait en parallèle. En un cycle horloge on envoie les données et on récupère le produit
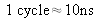 ce qui explique la rapidité du calcul.
ce qui explique la rapidité du calcul.