Formalisme matriciel optique intoduit par Abeles

L'introduction du formalisme matriciel est attribuée à Herpin pour l'optique des films minces homogènes []. Nous partons de l'article d'Abelès [] qui est repris dans de nombreux ouvrages de référence en optique [ ].

Un matériau stratifié introduit du point de vue optique une disymétrie entre la direction normale au film z et les directions x, y parallèles aux plans des surfaces. Ses caractéristiques sont invariantes par translation latérale, soit perpendiculaire à z et exprimées par l'indice de réfraction (optique ici): 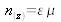. On distingue les régions suivantes du film :

Dans ce cas, nous devons repartir des équations de Maxwell pas encore simplifiées au cas des matériaux homogènes et qui se résument pour la polarisation "s" étudiée (Ey=Ez=0) à :

Combinées entre elles, elles conduisent à l'équation d'Helmoltz (déjà énoncée sous sa forme générale ) et qui se simplifie suivant les relations ci-dessus à l'expression :

Pour montrer que ce problème est unidimentionnel (selon z), Abelès propose comme solution de cette équation, un champ séparable en deux fonctions des directions y et z :

L'expression devient une égalité aux membres séparables :

Cette relation impose que ses deux membres soient egaux à une constante, et Abelès pose :

nous verrons que :

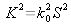
où K est une constante puisque 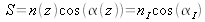est un invariant issu de la conservation de la composante tangentielle Ex au passage des différents dioptres de la multicouche (voir relations précédentes).

La première équation différentielle à des solutions du type 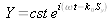. Un raisonnement analogue pour Hy et Hz conduit pour la polarisation "s" aux solutions :

Ces conditions se simplifient à deux équations différentielles du premier ordre après élimination de W. On obtient :

Notons que pour une onde polarisée "p" telle que Hy=Hz=0, on obtient des relations analogues en utilisant directement les substitutions vues précédemment sur cette équation.

Pour ces deux polarisations nous obtenons des équations différentielles linéaires du second ordre de type 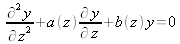. On en déduit que chaque solution U et V se décompose en combinaison linéaire de deux solutions particulières (U1, U2 ou V1, V2) satisfaisant le système d'équations linéaires du premier ordre introduit ci-dessus. On en déduit les systèmes suivants :

où l'exposant z fait référence à la différentiation selon z.

Cette égalité implique que le déterminant (Det) de deux solutions quelconques soit indépendant de z. Utilisons ce résultat en sélectionnant les deux solutions particulières suivantes :

Ainsi les solutions générales sont du type :

soit en notation matricielle :

On obtient la valeur de l'invariant traduisant la conservation de l'énergie au dioptre z=0 :

Par réciprocité, on en déduit la relation :

Rappelons que la connaissance de U et V revient respectivement à celle des champs Ex et Hy (pour la polarisation "s"). Ainsi la détermination de la matrice caractéristique M(z) du matériau stratifié permet de déterminer les composantes électriques et magnétiques de l'onde sinusoïdales dans les différentes strates (profondeur z) quand cette onde est connue dans le milieu incident. La matrice carrée M(z) est unimodulaire et ses éléments Mij dépendent uniquement de l'indice n(z) et donc de la structure du film en profondeur.