Expressions des vecteurs de diffusion pour leur calcul
La programmation des deux formalismes présentés (matriciel ou itératif) passe toujours par le calcul des vecteurs d'onde dans les différentes couches. Ces quantités pouvant être complexes, nous allons commencer par les définir et souligner une source d'erreur courante pour leur programmation. Revenons tout d'abord sur les relations de continuité des champs électromagnétiques aux interfaces qui lient les expressions des vecteurs d'onde du rayonnement se propageant de part et d'autre d'un dioptre. Ainsi le vecteur de diffusion dans la couche d'indice l+1 s'obtient à partir de sa valeur dans le milieu précédent d'indice l par la relation déjà vue :
Exprimons le module de ce vecteur autrement pour son calcul :
où l'angle critique attaché au dioptre entre les couches l et l+1 est repéré par la valeur du module du vecteur d'onde correspondant :
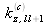. Pour calculer cette quantité complexe on utilise les relations la reliant aux indices ou densités de longueur de diffusion. Développons la somme en fonction des densité de longueur de diffusion :
En fonction des indices optiques on obtient :
Dans :
ou encore :
Pour ces expressions :
,
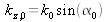et
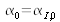est l'angle d'incidence du faisceau dans le milieu l=0 (vide) sur la surface.
Rappelons que la 2ième loi de descartes impose la conservation de la composante transverse des vecteurs d'onde soit :
La programmation de ces relations n'est pas aussi simple qu'il semble.
Pour un matériau sans absorption et à des angles inférieurs à son angle critique, la quantité sous la racine de l'expression du vecteur d'onde devient négative. Le vecteur d'onde dans le matériau est alors un imaginaire pur dont le signe doit être négatif en accord avec les conventions adoptées pour la dépendance temporelle et spatiale des champs électriques. Un logiciel tel que MATLAB [] prendra systématiquement cet imaginaire comme positif. Pour éviter cela il faut spécifier dans le calcul qu'on utilise son conjugué complexe. Dans le cas où de l'absorption existe, le vecteur de diffusion comporte toujours une partie imaginaire qui fixe son signe sans ambiguïté. Les effets de ces erreurs sont rarement spectaculaires dans les calculs des réflectivités car ils n'affectent que la partie imaginaire des coefficients de réflexion. Ils sont plus importants sous l'angle critique et lorsqu'on calcule des interférences entre ondes réfléchies.
C'est l'une des raisons pour lesquelles nous avons tracé systématiquement les phases des coefficients de réflectivité complexes (r) dans la suite.