Application aux films multicouches. Formalismes Dynamiques Discrets

Un système pouvant être décrit comme formé par l'empilement de couches homogènes d'indices optiques différents est dit multicouche. C'est un matériau stratifié particulier dont l'indice optique présente des discontinuités marquées selon l'axe z. Une telle multicouche est représenté sur la figure suivante. Chacune des N couches est numérotée (indice l) depuis le milieu d'incidence du faisceau correspondant à l'indice l=0 jusqu'au substrat d'indice l=N+1. Toutes ces strates d'épaisseurs respectives dl sont homogènes et caractérisées indifférament par leur indice optique nl ou leur densité de longueur de diffusion .

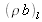Pour calculer la réflectivité R et la transmitivité T de cette multicouche, nous allons premièrement poursuivre le formalisme matriciel optique d'Abelès. Nous détaillerons ensuite l'utilisation de l'algorithme récursif de Parratt [] introduit pour la réflectivité des rayons-X mais issu du formalisme optique proposé par Airy pour une monocouche. Notons que Lord Rayleigh traitait de ce problème dès 1912 dans le cadre de la propagation des ondes acoustiques [].

Ces deux méthodes de calcul sont dynamiques et prennent en compte la réfraction et les réflexions multiples. Elles conservent l'énergie et peuvent être considérées comme exactes sur tout la gamme angulaire lorsque chaque interface de l'empilement multicouche satisfait les conditions de Fresnel énoncées précédemment pour un dioptre plan dit "idéal". Ces deux calculs conduisent aux mêmes résultats pour des diélectriques parfaits ( ).
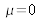