
Passage des films stratifiés aux multicouches avec le formalisme d'Abelès
Pour la propagation d'une onde sinusoïdale dans un milieu stratifié, la relation matricielle tient compte de la conservation des composantes tangentielles à l'axe de stratification (z) qui sont notées Ex et Hy. Comme nous l'avons vu, cette expression permet de lier les composantes de ces champs, à une profondeur donnée (U(z) et V(z)), à leur valeur dans le milieu d'incidence qui sont accessibles (U(0) et V(0)). Pour cela on doit déterminer la matrice M(z) qui caractérise la multicouche étudiée.
Dans le cas d'un simple dioptre, cette matrice permet de lier les valeurs des champs dans le milieu d'incidence I (UI(z>0) et VI(z>0)) à celles dans le matériau T (UT(z<0) et VT(z<0)) par la relation :
On généralise cette relation pour une multicouche quelconque caractérisée par la matrice M(z) et on lie les champs dans la couche N (UN(z) et VN(z) pour zN-1> z >zN) à ceux de l'onde incidente (U0(0) et V0(0) pour
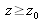 ) par la relation:
) par la relation:
et où la matrice Ml correspond à la couche
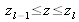 d'épaisseur
d'épaisseur
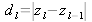 .
.
Examinons pour un tronçon l de cette multicouche la matrice Ml qui le caractérise. Partons du système qui devient :
Abelès indique que les solutions satisfaisant ces systèmes sont du type :
où A et B sont des constantes. On en déduit les solutions particulières introduites avant et qui nous conduisent aux éléments de la matrice Ml,ij caractérisant la couche l :
et où
Pl est appelé "admittance caractéristique" de la couche l par analogie avec l'électronique []. On passe aux résultats d'une polarisation "p" en appliquant les substitutions (
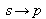 ).
).
Expérimentalement, les grandeurs accessibles se trouvent dans les milieux homogènes considérés comme semi-infinis indexés 0 (au dessus du film) et N+1 (au dessous du film) où s'effectue la mesure. Les grandeurs U(z=0) et V(z=0) correspondent aux champs dans le premier milieu qui peuvent s'obtenir par décomposition de ceux-ci en la somme de deux contributions correspondantes à une onde incidente (d'amplitude de champ électrique
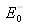 ) et à une onde réfléchie par la multicouche (d'amplitude de champ électrique
) et à une onde réfléchie par la multicouche (d'amplitude de champ électrique
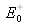 ). Ce qui se traduit par les égalités :
). Ce qui se traduit par les égalités :
Cette description du phénomène permet de revenir aux coefficients de réflexion
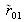 et de transmission
et de transmission
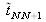 des milieux extrêmes :
des milieux extrêmes :
On en déduit la réflectivité R et transmission T de la multicouche (dans le milieu I = 0) :
Cas d'une couche homogène de diélectrique parfait
Supposons que la couche décrite par la figure précédente est non magnétique (
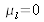 ) et purement diélectrique. On obtient alors :
) et purement diélectrique. On obtient alors :
Ces éléments sont introduits dans les équations donnant les coefficients en amplitude de réflexion et transmission de chaque interface. On obtient l'expression des coefficients de réflectivité et de transmission du film (notés avec une tilde). Elles se simplifient en introduisant les coefficients de Fresnel des interfaces. Pour le dioptre séparant le milieu I et T, ces coefficients deviennent :
En introduisant r12, r23 et t12, t23 dans les expressions de
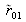 et
et
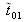 on retrouve les expressions de la réflectivité R et Transmission T déjà vues :
on retrouve les expressions de la réflectivité R et Transmission T déjà vues :