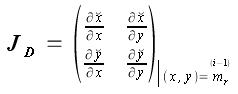Calibrage géométrique d'une caméra ou d'un capteur de vision stéréoscopique

Prise en compte des distorsions

Le modèle sténopé modélise une caméra idéale (simple projection perspective) et ne prend pas en compte les éventuelles distorsions géométriques induites par le système optique utilisé. Plusieurs auteurs [6, 7] ont montré que pour des applications de métrologie dimensionnelle, il était indispensable de prendre en compte ces distorsions afin de pouvoir les corriger.

Approche paramétrique (classique)

L'approche paramétrique classique consiste à modéliser la distorsion en enrichissant le modèle sténopé par des termes supplémentaires (le modèle devient alors non linéaire). Dans cette approche, le modèle s'inspire de la théorie des aberrations géométriques des systèmes centrés en rajoutant des termes correctifs correspondants à différents types de distorsions : distorsion radiale, prismatique, de décentrage [8, 9,10].

Partant du modèle sténopé, les effets des distorsions peuvent être modélisés par une quatrième transformation 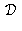, reliant les coordonnées rétiniennes « idéales (2.) » 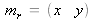aux coordonnées rétiniennes « réelles » :

Figure 4 : Prise en compte de la distorsion dans le modèle par la transformation D [zoom...]

(8)

Plusieurs auteurs ont montré que le modèle suivant, souvent désigné par R3D1P1 (3.) , est largement suffisant pour la plupart des objectifs de focale supérieure à 5 mm :

(9)

Où est le vecteur des paramètres de distorsion.

On se contente souvent d'utiliser un modèle radial (d'ordre 1 à 3). En posant : 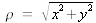, le modèle R3, est souvent écrit sous la forme :

(10)

Notons 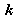le vecteur des paramètres intrinsèques définis par la matrice 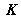, et le vecteur des coefficients de distorsion (qui sont également intrinsèques à la caméra) :

Le modèle de caméra est non linéaire et peut s'écrire sous la forme d'une fonction vectorielle :

(11)

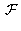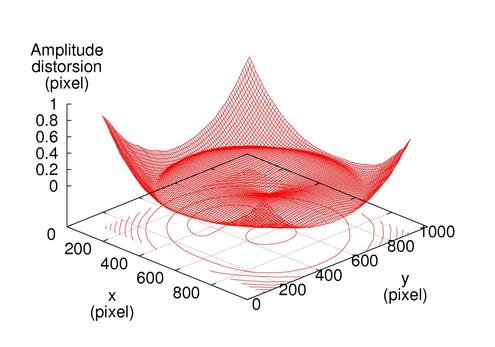
À titre d'exemple, la figure 5 montre une carte de distorsion (amplitude de la distorsion en chaque pixel de l'image) obtenue lors du calibrage d'une caméra équipée d'un objectif de focale 25 mm. On voit bien sur cette figure que la composante dominante est la distorsion radiale (distorsion d'autant plus importante qu'on s'éloigne du centre de l'image). Dans cet exemple, la distorsion est relativement faible (l'amplitude de la distorsion est de l'ordre de 1 pixel aux coins de l'image) mais elle peut atteindre plusieurs pixels (voire dizaine de pixels) pour des objectifs de plus faible longueur focale.

Figure 5 : Carte des distorsions : l'amplitude de la distorsion est de l'ordre de 1 pixel aux coins de l'image [zoom...]

Correction de la distorsion

Il est parfois nécessaire de connaître les coordonnées pixel idéales 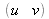, i.e. non distordues, correspondant à celles distordues .

(12)

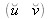On en déduit que :

(13)

À partir des équations (12) et (13), on constate qu'il est possible d'exprimer 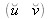en fonction de 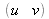et des paramètres intrinsèques et de la caméra :

(14)

Dans le cas général, le modèle de distorsion donné par l'équation (14) n'est pas inversible et il est donc nécessaire d'utiliser une méthode numérique pour estimer les coordonnées idéales 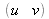du point-image qui aurait été obtenu avec une caméra exempte de distorsion.

Soit 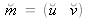un pixel de l'image distordue. On cherche le pixel non distordu .

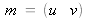Le pixel 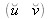correspond au point dans le plan rétinien :

On cherche le point tel que :

(15)

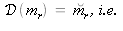On peut résoudre l'équation (15) grâce à la méthode de Newton appliquée à la fonction 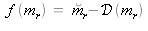que l'on initialise avec .

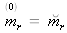L'itéré courant est donné par la formule :

Soit :

(16)

avec :

[zoom...]

Le critère d'arrêt peut être basé sur la valeur du module de l'erreur 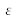après chaque itération. En pratique, la convergence est atteinte après seulement quelques itérations .

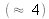Après avoir obtenu les coordonnées rétiniennes 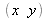, l'équation (12) permet de calculer les coordonnées 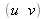recherchées.

Pour calculer une image corrigée de la distorsion (ce qui est un problème différent de celui de corriger un seul point), il n'est pas nécessaire de recourir à une méthode numérique pour inverser le modèle de distorsion. Il suffit d'utiliser le modèle direct donné par l'équation (14) et de remplir l'image à construire en balayant les coordonnées 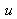et 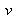de l'image destination.

Pour un pixel 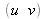donné (en coordonnées entières) dans l'image destination, l'équation (14) permet de calculer les coordonnées du point correspondant dans l'image source. Ces coordonnées étant en général non entières, il suffit de faire une interpolation pour calculer la valeur de l'intensité (niveau de gris) qui doit être recopiée dans l'image destination à la position 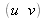(cf. [11]).

D'autres méthodes de correction de distorsion ont été proposées dans la littérature. Pour un état de l'art récent, voir en particulier la section « The perspective camera inverse model » dans [12].

À titre d'exemple, la figure 6 montre une image distordue (à gauche) et l'image corrigée (à droite).

Figure 6 : Une image distordue (à gauche) et l'image corrigée (à droite) [zoom...]

Approche non-paramétrique

Dans le cas de systèmes optiques complexes, certains auteurs ont montré [13] qu'il est préférable de modéliser la distorsion de façon non-paramétrique en utilisant des fonctions splines [14].

Dans ce cas, il s'agit d'une modélisation purement mathématique (approche type « boîte noire ») visant à déterminer la fonction de distorsion qui traduit au mieux la façon dont l'image idéale est distordue [15 16].

S'agissant d'une modélisation purement mathématique (4.), il n'est pas gênant d'adopter dans ce cas le schéma de la figure 7, et de rechercher la fonction de distorsion reliant les coordonnées-image idéales du point 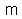aux coordonnées-image réelles 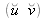du point .

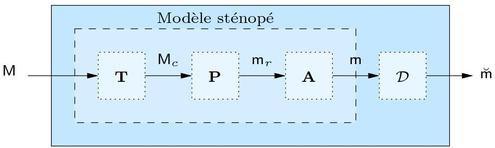
Figure 7 : Modèle de caméra avec distorsion non paramétrique [zoom...]

Dans cette approche, pour pouvoir corriger facilement la distorsion, il est préférable d'adopter le modèle schématisé sur la figure 8, dans lequel on utilise la fonction réciproque de correction de distorsion au lieu de la fonction de distorsion . En effet, utiliser présente l'avantage de permettre de corriger directement la distorsion alors qu'inverser la fonction 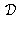peut être très coûteux en temps de calcul, notamment lorsque sa fonction réciproque ne peut pas être déterminée analytiquement. De plus, le domaine de définition de la fonction spline de correction est connu a priori et déterminé par la dimension des images, alors que la fonction spline de distorsion 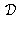a un domaine de définition non connu a priori puisque exprimé dans le plan rétinien lui-même défini par calibrage.

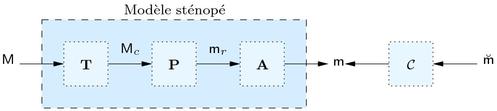
Figure 8 : Modèle de caméra avec correction de la distorsion non paramétrique [zoom...]

L'équation de correction de distorsion devient :

(17)

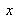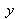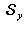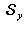L'estimation de la fonction de correction de distorsion consiste à approximer les composantes horizontales (suivant l'axe ) et verticales (suivant l'axe ) du champ de correction de distorsion par deux surfaces splines et [13, 17].

La fonction de correction de distorsion permet de corriger les points (ou une image entière) des distorsions. Les points ainsi corrigés sont reliés aux point 3D d'entrée par un modèle sténopé classique dont il est facile d'estimer les paramètres.

Nous venons d'établir les modèles linéaire (5) et non linéaire (11) d'une caméra, nous allons parler maintenant des méthodes dites de calibrage permettant d'estimer les paramètres de ces modèles.

AccueilOutils transversesNouvelle pageInformations sur le cours (ouvrir dans une nouvelle fenêtre)Modèle sténopé completCalibrage