
Calibrage
Calibrer une caméra consiste à estimer les paramètres du modèle qui a été choisi pour la représenter. C'est un problème d'estimation paramétrique.
Dans le cas du modèle sténopé (avec ou sans distorsion), il s'agit d'estimer les paramètres intrinsèques de la caméra, et sa position et orientation par rapport au repère du monde qui a été choisi (paramètres extrinsèques).
A vrai dire, lorsqu'on calibre une caméra, c'est essentiellement pour déterminer ses paramètres intrinsèques qui, comme leur nom l'indique, sont intrinsèques à la caméra et ne changent pas si l'on déplace la caméra. Des méthodes spécifiques (dites de localisation) ont été développées pour déterminer la position d'une caméra par rapport à un repère de travail lorsqu'on connaît déjà ses paramètres intrinsèques.
Généralement, ce problème de calibrage est résolu en utilisant un objet de calibrage spécifique (mire) qui fournit des points 3D connus dans le repère du monde.
De nombreuses méthodes de calibrage ont été proposées. Au fil des années, ces méthodes sont devenues de plus en plus sophistiquées pour conduire à un calibrage de plus en plus précis, tout en étant de plus en plus facile à mettre en œuvre.
Nous allons décrire dans ce qui suit la méthode qui est considérée aujourd'hui comme la plus performante.
La méthode consiste à acquérir
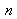 images d'une mire (plane (5.)) composée de
images d'une mire (plane (5.)) composée de
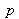 points déplacée librement (rotations et translations) dans le champ de vue de la caméra (cf. figure 9). La méthode de calibrage qui va être décrite est dite de type photogrammétrique. Elle permet d'estimer en même temps tous les paramètres du modèle de caméra ainsi que les points tridimensionnels de la mire. Par conséquent, la géométrie de la mire de calibrage n'a pas besoin d'être connue avec précision a priori.
points déplacée librement (rotations et translations) dans le champ de vue de la caméra (cf. figure 9). La méthode de calibrage qui va être décrite est dite de type photogrammétrique. Elle permet d'estimer en même temps tous les paramètres du modèle de caméra ainsi que les points tridimensionnels de la mire. Par conséquent, la géométrie de la mire de calibrage n'a pas besoin d'être connue avec précision a priori.
Lors du déplacement de la mire de calibrage, il est important de bien couvrir l'ensemble du champ de vue de la caméra de façon à calibrer correctement la distorsion (qui est généralement plus importante au bord des images qu'au centre).
Les points de la mire peuvent être les nœuds d'intersections de droites horizontales et verticales (grille), les coins d'une mire de damiers, ou bien les centres de taches circulaires.
Les points de la mire, qui sont extraits par des procédures spécifiques de traitement d'images, fournissent les mesures.
La figure 9 illustre une séquence de 6 images d'une mire de calibrage composée de 64 taches circulaires.

On note
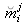 les coordonnées de la projection du
les coordonnées de la projection du
 point
point
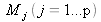 de la
de la
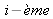 vue
vue
 sur le plan image de la caméra. Si la distorsion est prise en compte, nous pouvons écrire à partir de (11) :
sur le plan image de la caméra. Si la distorsion est prise en compte, nous pouvons écrire à partir de (11) :
Dans ces équations, le référentiel de la mire est utilisé pour chaque vue comme référentiel du monde, (cf. figure 10).

En utilisant (18), chaque projection d'un point tridimensionnel fournit deux équations. Il y a donc
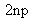 équations.
équations.
Comptabilisons les paramètres inconnus à estimer : cinq paramètres intrinsèques, sept paramètres de distorsion dans le cas d'un modèle R3D1P1,
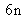 paramètres extrinsèques (trois pour la rotation et trois autres pour la translation de chaque transformation rigide
paramètres extrinsèques (trois pour la rotation et trois autres pour la translation de chaque transformation rigide
 ) et
) et
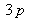 coordonnées tridimensionnelles. Cela donne un total de
coordonnées tridimensionnelles. Cela donne un total de
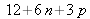 inconnues.
inconnues.
Il y a donc
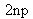 équations et
équations et
 inconnues. Si
inconnues. Si
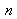 et
et
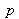 sont suffisamment grands (par exemple si
sont suffisamment grands (par exemple si
 et
et
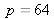 , il y a 768 équations pour 240 inconnues) nous pouvons estimer tous les paramètres en minimisant la somme des distances entre la projection du
, il y a 768 équations pour 240 inconnues) nous pouvons estimer tous les paramètres en minimisant la somme des distances entre la projection du
 point de la
point de la
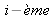 vue dans l'image et le point
vue dans l'image et le point
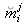 correspondant extrait dans l'image :
correspondant extrait dans l'image :
avec
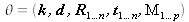 .
.
Minimiser (19) est un problème d'optimisation non linéaire (appelé ajustement de faisceaux ou « bundle adjustment » en anglais [18]).
Le problème est habituellement résolu en utilisant l'algorithme de Levenberg- Marquardt [19], avec les rotations
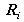 exprimées sous une forme minimale (vecteur rotation instantanée, angles d'Euler, angles de Bryant, etc.).
exprimées sous une forme minimale (vecteur rotation instantanée, angles d'Euler, angles de Bryant, etc.).
Pour pouvoir converger, l'algorithme de minimisation nécessite des estimées initiales des paramètres recherchés : les estimées des cinq paramètres intrinsèques du modèle sténopé et des paramètres extrinsèques peuvent être obtenues par des méthodes analytiques décrites dans [20 , 21]. Les paramètres de distorsion sont généralement initialisés à zéro. Les coordonnées tridimensionnelles initiales des points de la mire sont celles de son modèle ayant servi à sa réalisation. Étant donné qu'elles seront réestimées, ces coordonnées n'ont pas besoin d'être connues avec précision, ce qui représente un avantage par rapport aux méthodes nécessitant une connaissance précise de la mire de calibrage utilisée.
La minimisation de (19) conduit à une solution définie à un facteur d'échelle près. Celui-ci peut être déterminé en fournissant la distance mesurée dans l'espace entre deux points donnés (2 points particuliers de la mire par exemple).